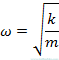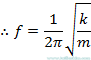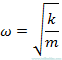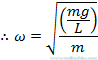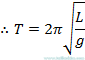Basit Harmonik Hareket Formülleri fizik için önemli formüllerdendir, bunların kullanım alanları ve kısa ve basit formüllerinden sizlere açıklamaya çalışacağız.
Basit Harmonik Hareket Nedir?
Konu Anlatımı
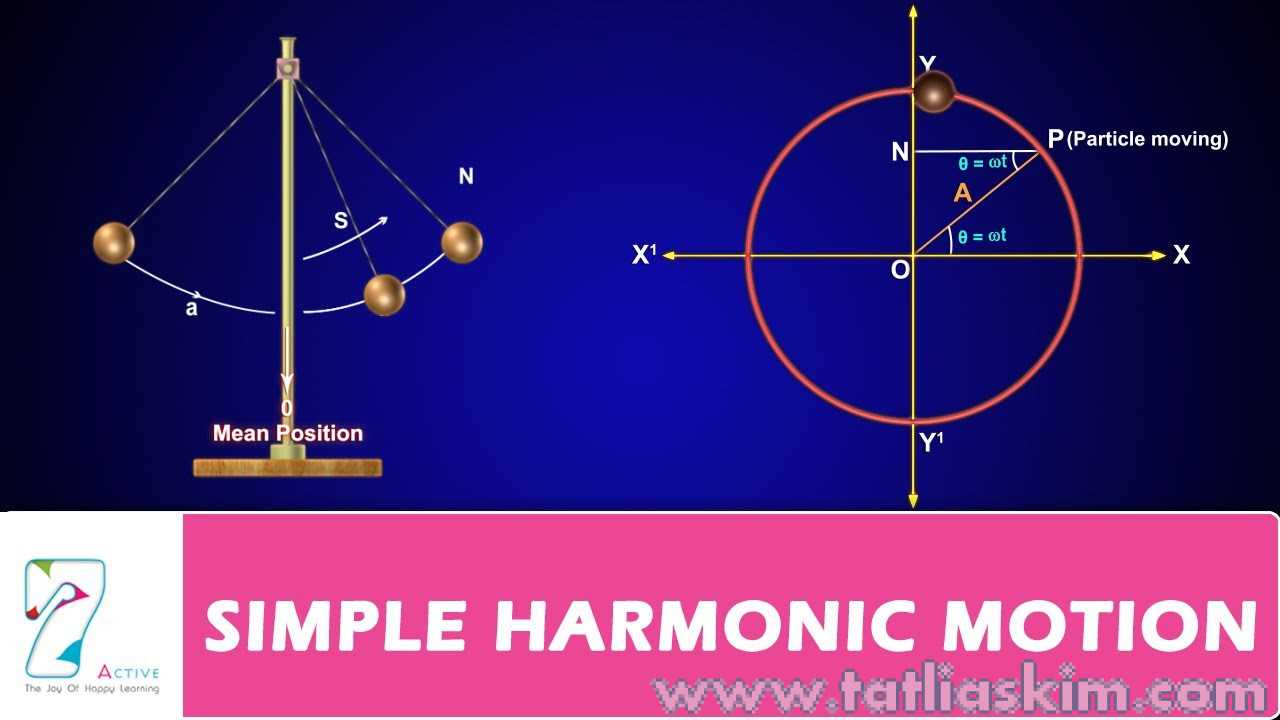
Bir nesne, hareketi tanımlanmış bir döngüde tekrarlandığında periyodik olarak hareket eder. Periyodik hareket de salınım olarak bilinir. Yaygın örnekler yayların ve sarkaçların hareketidir, ancak salınımların meydana geldiği birçok durum vardır.
Periyodik hareketin en önemli özellikleri, nesnenin dengeli bir denge konumuna ve o konuma doğru yönlendirilen bir geri yükleme kuvvetine sahip olmasıdır. Yaylar için, dinlenecekleri bir pozisyon vardır, ancak ya gerilmiş ya da sıkıştırılmış olduklarında, denge pozisyonu yönünde her zaman işaret edilen bir geri yükleme kuvveti vardır. Sarkaçlar düz bir şekilde asıldıklarında stabildir. Bir sarkaç bu denge konumundan uzaklaştırılırsa, gerginlik kuvveti ve yerçekimi tarafından etkilendiği için ileri ve geri sallanır.
Denge pozisyonu orijin, O olarak tanımlanır. Belli bir kütle m’ye sahip bir nesne orijin üzerinde başlar ve ondan uzaklaşırsa, hareketinin mesafesi yer değiştirir. X-eksenindeki tek boyutlu hareket için, yer değiştirme x değişkenine atanabilir. Geri itme kuvveti F x Bu eksende hareket eder. X eksenindeki x ivme Newton’un ikinci kanunu tarafından bulunabilir,
Bir boyutta salınan bir nesne, orijin üzerinden ileri geri hareket edecektir. İdeal (veya basit) durumda, her iki yönde de aynı mesafeyi orijinden uzaklaştıracaktır. Bu değer “genlik” olarak adlandırılır ve A değişkenine atanır. Nesnenin periyodik hareketi x = A ve x = -A arasında sınırlandırılır. Bir yer değiştirme olduğundan, A’nın SI birimi metredir.
Bir nesnenin tam bir salınımı “döngü” olarak adlandırılır. Bir döngüde, nesne, deplasman A’dan, orijinale -A ve A’ya geri dönebilir. Nesne, o pozisyona geri döndüğü sürece, başlangıç noktası önemli değildir. O’dan A’ya, -A’ya ve O’ya geri hareket eden nesne de bir döngüdür.
Nesnenin bir döngü içinde hareket etmesi için gereken süre “periyot”, T olarak adlandırılır. Periyot için SI birimi ikinci olur, ancak “devir başına saniye” genellikle yazılır. “Döngü” ünün bir birim olmadığını hatırlamak önemlidir, bu nedenle bu şekilde kullanılması yalnızca yer tutucu işlevi görür veya zamanın periyodik hareketle ilgili olduğunu hatırlatır.
Dönemin tersi “frekans” olarak adlandırılır. F frekansı
Bu nedenle şu periyottadır.
.
Frekans birimi birkaç yolla yazılabilir. “Devir / saniye” genellikle yazılır, ancak “döngü” nin kendisinin bir birim olmadığını hatırlayın. Bu, SI frekansı birim yapar veya
. Bu birim “Hertz” (Hz) olarak da adlandırılır, burada
başka bir faydalı miktar “. Açısal frekans, frekansın 2π katına eşittir
,
Açısal frekans , döneme göre de ifade edilebilir, Açısal frekans, bir açının değişim oranını temsil eder. Periyodik hareketin açılışı ve açıları arasındaki bağlantı, periyodik hareketin “döngüleri” ni daire etrafında hareket olarak düşünerek hayal etmek daha kolaydır. Tam bir daire içinde açıların aralığı öyle
. Yani, f frekansı birimi ise
, o zaman açısal frekans birimi olur
.Basit Harmonik Hareket
Basit Harmonik Hareket (SHM), periyodik hareket özel bir durumdur. SHM’de geri yükleme gücü F xdeplasman x ile doğru orantılıdır. Geri çekme kuvveti ve deplasmanın her zaman zıt işaretleri vardır, çünkü kuvvet daima köke doğrudur. Bir orantılılık sabiti, kuvvet için bir denklem yazmayı mümkün kılar,
Yaylar için, bu ilişki Hooke Yasası olarak bilinir ve k, yay sabiti olarak adlandırılır. K’nin SI birimi metre başına Newton’dur .
Basit harmonik hareket halindeki bir nesnenin ivme Newton’un ikinci kanunu ve Hooke yasası birleştirilerek bulunabilir,
ve
, basit harmonik hareket açısal frekansı sadece yay sabiti ve nesnenin kütlesine bağlı olduğu bir sabittir
Basit Harmonik Hareket Formülleri
Bu denklemi ve açısal frekansa ilişkin denklemleri bu bölümde daha önceki döneme ve frekansa ilişkin olarak kullanarak, basit harmonik harekette frekans ve periyot için formüller elde edilebilir
ve
Basit harmonik hareketle, bir nesnenin yer değiştirmesi, Zamanında sinüzoidal bir fonksiyon. Bu fonksiyonlar (sinüs veya kosinüs) periyodik veya döngüsel durumları tanımlamak için idealdir ve basit harmonik hareket zamana göre döngüsel bir davranışa sahiptir. Bir nesnenin basit harmonik hareketle yer değiştirmesi için genel denklem yazılabilir
. Bu denklemde A, bu bölümde daha önce tanımlanmış olan hareketin genliğidir. Saniye cinsinden süre t değişkenidir. Bir “faz açısı” varradyan birimleri var. Faz açısı, başlangıç pozisyonunun bir seçimini temsil eder. Salınım yapan nesnenin başlangıç zamanındaki konumuyla ayarlanır, t = 0. Başlangıç konumu x = A ise, o zaman faz açısı olur
. Başlangıç pozisyonu x = 0 m ise, faz açısı
Basit Harmonik Harekette Enerji’dir.
Basit harmonik hareketlerdeki nesneler için toplam mekanik enerji korunur. Bu, sistemin enerjisinin kinetik (K) ve potansiyel (U) enerji arasında gidip geldiği ve bunların toplamının her zaman sabit
olduğu anlamına gelir. Nesnenin kinetik enerjisi hızı ile ilgilidir
. Potansiyel enerji basit harmonik harekette nesnenin
toplamı, bunların toplamı hareketin genliği ile ilgilidir.
Dikey Yaylar
Bir yayın bir ucunun bir kancaya takılı olduğunu ve diğerinin de kütle m ile bir nesneye bağlı olduğunu ve dikey olarak asılmasına izin verdiğini düşünün. Bu durumda, nesne iki güçle karşılaşır. Bir kuvvet, yukarı doğru yönlendirilmiş, yayın geri yükleme kuvveti olacaktır. Diğer güç, kütle üzerinde hareket eden ve aşağıya doğru yönlendirilen yerçekimi kuvveti olacaktır. Eğer kütle hareket etmiyorsa, net kuvvetin sıfır olduğu bir denge konumunda duracak,
eğer “yukarı” pozitif x yönü olarak tanımlanırsa ve x = 0 pozisyonu denge pozisyonunun üstündeyse, o zaman toplam x eksenindeki kuvvetlerin,
Denge pozisyonu kuvvetlerin toplamı için yukarıdaki formülden bulunabilir.
Basit Sarkaç
Sarkaçlar düz bir şekilde asıldıklarında stabildir. Bu konumda, çubuk veya ipin ucundaki kütle, iki kuvvet tarafından etkindir. Bunlar, çubuk veya iplikte gerginlik kuvveti ve yerçekimine bağlı kuvvetlerdir. Denge konumunda, bu kuvvetler sıfıra düşer. Bir sarkaç denge konumundan uzaklaştırılırsa, denge noktasından ileri geri hareket eder. Çubuk dikey ekseni ile yaptığı açı θ ise, geri getirme kuvveti, yerçekimi kuvvetinin bir bileşeni olan
açı θ küçük ise, küçük açı yaklaşımı , sinθ formülünü kolaylaştırmak için kullanılabilir
( θ açısı küçük olduğunda)
Çubuğun uzunluğu L ise ve yatay eksende yer değiştirme x ise,
Küçük açı yaklaşımıyla, geri yükleme kuvveti şu
şekildedir: Bu, yaylar için yay geri yükleme kuvveti şeklindedir, F = -kx. Bu nedenle, x’in önündeki değerler yay sabitine eşittir, k,
Basit bir sarkaç için açısal frekans, Basit bir sarkaçın
salınım sıklığıdır, Basit bir sarkaçın
salınım periyodu,
Basit Harmonik Hareket Soru Çözümü
Sizler de yorumlarda bu konu ile alakalı çözümlerinizi bizler ile paylaşırsanız bu konuyu anlamayanlar için çözümler herkese faydalı olacaktır. Soruları ve Ders notları paylaşabilirsiniz.